7  Teori Portofolio Modern

Teori Markowitz dalam Optimasi Portofolio

Pendahuluan

Teori Portofolio Modern (Modern Portfolio Theory/MPT) dikembangkan oleh Harry Markowitz pada tahun 1952 dalam paper seminalnya “Portfolio Selection” yang dipublikasikan di Journal of Finance. Teori ini merevolusi cara investor memandang risiko dan return dalam investasi, dan Markowitz dianugerahi Nobel Prize in Economics pada tahun 1990 atas kontribusinya.

Konsep Dasar

MPT didasarkan pada premis bahwa investor adalah risk-averse, yang berarti:

• Investor menginginkan return maksimal untuk tingkat risiko tertentu
• Investor menginginkan risiko minimal untuk tingkat return tertentu
• Investor membuat keputusan berdasarkan expected return dan risiko (variance/standard deviation)

Asumsi-Asumsi MPT

1. Pasar Efisien: Semua informasi tersedia dan tercermin dalam harga
2. Investor Rasional: Investor membuat keputusan berdasarkan expected utility
3. Distribusi Normal: Return aset mengikuti distribusi normal
4. Single Period: Analisis dilakukan untuk satu periode investasi
5. Risk Aversion: Investor menghindari risiko
6. No Transaction Costs: Tidak ada biaya transaksi atau pajak

8 Komponen Fundamental

Expected Return Portofolio

Expected return portofolio adalah rata-rata tertimbang dari expected return masing-masing aset:

\[E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\]

Dimana:

• \(E(R_p)\) = Expected return portofolio
• \(w_i\) = Bobot/proporsi aset i dalam portofolio
• \(E(R_i)\) = Expected return aset i
• \(n\) = Jumlah aset dalam portofolio
• \(\sum_{i=1}^{n} w_i = 1\) (total bobot = 100%)

Risiko Portofolio (Variance dan Standard Deviation)

Risiko portofolio diukur dengan variance atau standard deviation. Untuk portofolio dengan 2 aset:

\[\sigma_p^2 = w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2\sigma_1\sigma_2\rho_{12}\]

Atau:

\[\sigma_p^2 = w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2Cov(R_1,R_2)\]

Untuk portofolio dengan n aset:

\[\sigma_p^2 = \sum_{i=1}^{n}\sum_{j=1}^{n}w_iw_j\sigma_{ij}\]

Dimana:

• \(\sigma_p^2\) = Variance portofolio
• \(\sigma_p\) = Standard deviation portofolio = \(\sqrt{\sigma_p^2}\)
• \(\rho_{ij}\) = Korelasi antara aset i dan j
• \(\sigma_{ij}\) = Covariance antara aset i dan j
• \(Cov(R_i,R_j) = \rho_{ij}\sigma_i\sigma_j\)

Diversifikasi

Prinsip Kunci: Risiko portofolio tidak hanya bergantung pada risiko individual aset, tetapi juga pada korelasi antar aset.

Manfaat Diversifikasi

• Korelasi Negatif (\(\rho < 0\)): Diversifikasi sangat efektif
• Korelasi Nol (\(\rho = 0\)): Diversifikasi mengurangi risiko
• Korelasi Positif Sempurna (\(\rho = +1\)): Tidak ada manfaat diversifikasi

Jenis Risiko

1. Systematic Risk (Market Risk): Risiko yang tidak dapat dihilangkan dengan diversifikasi
2. Unsystematic Risk (Specific Risk): Risiko yang dapat dihilangkan dengan diversifikasi

9 Efficient Frontier

Konsep Efficient Frontier

Efficient Frontier adalah kumpulan portofolio yang memberikan:

• Expected return maksimal untuk tingkat risiko tertentu, atau
• Risiko minimal untuk tingkat expected return tertentu

import numpy as np
import matplotlib.pyplot as plt

# Set random seed untuk reprodusibilitas
np.random.seed(42)

# Generate random portfolios
n_portfolios = 10000
returns = np.random.uniform(0.05, 0.20, n_portfolios)
risks = np.random.uniform(0.05, 0.30, n_portfolios)

# Filter untuk efficient frontier (simplified)
sorted_indices = np.argsort(risks)
returns_sorted = returns[sorted_indices]
risks_sorted = risks[sorted_indices]

# Efficient frontier (upper envelope)
efficient_returns = []
efficient_risks = []
max_return = -np.inf

for risk, ret in zip(risks_sorted, returns_sorted):
    if ret > max_return:
        efficient_risks.append(risk)
        efficient_returns.append(ret)
        max_return = ret

# Plot
plt.figure(figsize=(10, 6))
plt.scatter(risks, returns, alpha=0.3, s=10, label='Portofolio Feasible')
plt.plot(efficient_risks, efficient_returns, 'r-', linewidth=2, label='Efficient Frontier')
plt.xlabel('Risiko (Standard Deviation)', fontsize=12)
plt.ylabel('Expected Return', fontsize=12)
plt.title('Efficient Frontier - Teori Markowitz', fontsize=14, fontweight='bold')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

Figure 9.1: Ilustrasi Efficient Frontier

Karakteristik Portofolio Optimal

Minimum Variance Portfolio (MVP)

Portofolio dengan risiko terendah pada efficient frontier.

Maximum Sharpe Ratio Portfolio

Portofolio dengan rasio return-to-risk tertinggi:

\[\text{Sharpe Ratio} = \frac{E(R_p) - R_f}{\sigma_p}\]

Dimana \(R_f\) adalah risk-free rate.

10 Optimasi Portofolio Markowitz

Formulasi Masalah Optimasi

Minimize Risk untuk Target Return

\[\min_{w} \quad \sigma_p^2 = \sum_{i=1}^{n}\sum_{j=1}^{n}w_iw_j\sigma_{ij}\]

Subject to:

\[\sum_{i=1}^{n} w_i E(R_i) = R_p^*\] \[\sum_{i=1}^{n} w_i = 1\] \[w_i \geq 0 \quad \forall i \quad \text{(optional: no short selling)}\]

Maximize Sharpe Ratio

\[\max_{w} \quad \frac{E(R_p) - R_f}{\sigma_p}\]

Subject to:

\[\sum_{i=1}^{n} w_i = 1\] \[w_i \geq 0 \quad \forall i \quad \text{(optional)}\]

Contoh Perhitungan Manual

Data Input

Misalkan kita memiliki 2 aset dengan karakteristik:

Aset	Expected Return	Std. Dev
A	12%	20%
B	8%	10%

Korelasi: \(\rho_{AB} = 0.3\)

Perhitungan untuk Berbagai Bobot

import pandas as pd

# Data
r_A, r_B = 0.12, 0.08
sigma_A, sigma_B = 0.20, 0.10
rho_AB = 0.3
cov_AB = rho_AB * sigma_A * sigma_B

# Berbagai kombinasi bobot
weights_A = np.arange(0, 1.1, 0.1)
weights_B = 1 - weights_A

# Hitung return dan risiko portofolio
portfolio_returns = weights_A * r_A + weights_B * r_B
portfolio_variance = (weights_A**2 * sigma_A**2 + 
                     weights_B**2 * sigma_B**2 + 
                     2 * weights_A * weights_B * cov_AB)
portfolio_std = np.sqrt(portfolio_variance)

# Buat DataFrame
df = pd.DataFrame({
    'Bobot A': weights_A,
    'Bobot B': weights_B,
    'E(Rp)': portfolio_returns,
    'σp': portfolio_std,
    'σp²': portfolio_variance
})

df.style.format({
    'Bobot A': '{:.1f}',
    'Bobot B': '{:.1f}',
    'E(Rp)': '{:.4f}',
    'σp': '{:.4f}',
    'σp²': '{:.6f}'
})

Table 10.1: Perhitungan Return dan Risiko Portofolio

	Bobot A	Bobot B	E(Rp)	σp	σp²
0	0.0	1.0	0.0800	0.1000	0.010000
1	0.1	0.9	0.0840	0.0979	0.009580
2	0.2	0.8	0.0880	0.0996	0.009920
3	0.3	0.7	0.0920	0.1050	0.011020
4	0.4	0.6	0.0960	0.1135	0.012880
5	0.5	0.5	0.1000	0.1245	0.015500
6	0.6	0.4	0.1040	0.1374	0.018880
7	0.7	0.3	0.1080	0.1517	0.023020
8	0.8	0.2	0.1120	0.1671	0.027920
9	0.9	0.1	0.1160	0.1832	0.033580
10	1.0	0.0	0.1200	0.2000	0.040000

Visualisasi Risk-Return Tradeoff

plt.figure(figsize=(10, 6))
plt.plot(portfolio_std, portfolio_returns, 'b-o', linewidth=2, markersize=6)
plt.scatter([sigma_A, sigma_B], [r_A, r_B], s=200, c='red', marker='*', 
           label='Individual Assets', edgecolors='black', linewidths=2)
plt.xlabel('Risiko Portofolio (σp)', fontsize=12)
plt.ylabel('Expected Return Portofolio', fontsize=12)
plt.title('Risk-Return Combinations: Two-Asset Portfolio', fontsize=14, fontweight='bold')
plt.legend()
plt.grid(True, alpha=0.3)

# Annotate assets
plt.annotate('Asset A', (sigma_A, r_A), xytext=(sigma_A+0.01, r_A+0.005),
            fontsize=10, fontweight='bold')
plt.annotate('Asset B', (sigma_B, r_B), xytext=(sigma_B+0.01, r_B-0.005),
            fontsize=10, fontweight='bold')

plt.show()

Figure 10.1: Risk-Return Tradeoff untuk 2 Aset

11 Implementasi dengan Python

Setup dan Library

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.optimize import minimize
import warnings
warnings.filterwarnings('ignore')

# Set style
plt.style.use('seaborn-v0_8-darkgrid')
sns.set_palette("husl")

Fungsi-Fungsi Utama

def portfolio_return(weights, returns):
    """Hitung expected return portofolio"""
    return np.dot(weights, returns)

def portfolio_variance(weights, cov_matrix):
    """Hitung variance portofolio"""
    return np.dot(weights.T, np.dot(cov_matrix, weights))

def portfolio_std(weights, cov_matrix):
    """Hitung standard deviation portofolio"""
    return np.sqrt(portfolio_variance(weights, cov_matrix))

def portfolio_sharpe(weights, returns, cov_matrix, risk_free_rate=0.02):
    """Hitung Sharpe Ratio"""
    p_return = portfolio_return(weights, returns)
    p_std = portfolio_std(weights, cov_matrix)
    return (p_return - risk_free_rate) / p_std

def negative_sharpe(weights, returns, cov_matrix, risk_free_rate=0.02):
    """Negative Sharpe Ratio untuk optimasi (minimize)"""
    return -portfolio_sharpe(weights, returns, cov_matrix, risk_free_rate)

Simulasi Data Historis

# Simulasi return untuk 4 aset
np.random.seed(123)
n_days = 1000
n_assets = 4

# Generate random returns
returns_data = np.random.randn(n_days, n_assets) * 0.02 + np.array([0.0003, 0.0002, 0.0004, 0.0001])

# Buat DataFrame
assets = ['Saham A', 'Saham B', 'Saham C', 'Obligasi']
df_returns = pd.DataFrame(returns_data, columns=assets)

# Hitung statistik
mean_returns = df_returns.mean() * 252  # Annualized
cov_matrix = df_returns.cov() * 252     # Annualized

print("Expected Annual Returns:")
print(mean_returns)
print("\nCovariance Matrix:")
print(cov_matrix)

Expected Annual Returns:
Saham A     0.037791
Saham B     0.247768
Saham C     0.048956
Obligasi    0.147595
dtype: float64

Covariance Matrix:
           Saham A   Saham B   Saham C  Obligasi
Saham A   0.096221  0.000419  0.004668 -0.003356
Saham B   0.000419  0.095525  0.000222 -0.006813
Saham C   0.004668  0.000222  0.103281  0.006440
Obligasi -0.003356 -0.006813  0.006440  0.094925

Optimasi Portofolio

Minimum Variance Portfolio

n_assets = len(mean_returns)

# Constraint: sum of weights = 1
constraints = {'type': 'eq', 'fun': lambda x: np.sum(x) - 1}

# Bounds: 0 <= weight <= 1 (no short selling)
bounds = tuple((0, 1) for _ in range(n_assets))

# Initial guess
initial_weights = np.array([1/n_assets] * n_assets)

# Optimize untuk Minimum Variance
result_mvp = minimize(
    fun=lambda w: portfolio_variance(w, cov_matrix),
    x0=initial_weights,
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

mvp_weights = result_mvp.x
mvp_return = portfolio_return(mvp_weights, mean_returns)
mvp_std = portfolio_std(mvp_weights, cov_matrix)

print("Minimum Variance Portfolio:")
print("-" * 50)
for asset, weight in zip(assets, mvp_weights):
    print(f"{asset}: {weight:.4f} ({weight*100:.2f}%)")
print(f"\nExpected Return: {mvp_return:.4f} ({mvp_return*100:.2f}%)")
print(f"Standard Deviation: {mvp_std:.4f} ({mvp_std*100:.2f}%)")

Minimum Variance Portfolio:
--------------------------------------------------
Saham A: 0.2508 (25.08%)
Saham B: 0.2731 (27.31%)
Saham C: 0.2067 (20.67%)
Obligasi: 0.2694 (26.94%)

Expected Return: 0.1270 (12.70%)
Standard Deviation: 0.1559 (15.59%)

Maximum Sharpe Ratio Portfolio

risk_free_rate = 0.02

# Optimize untuk Maximum Sharpe Ratio
result_sharpe = minimize(
    fun=negative_sharpe,
    x0=initial_weights,
    args=(mean_returns, cov_matrix, risk_free_rate),
    method='SLSQP',
    bounds=bounds,
    constraints=constraints
)

sharpe_weights = result_sharpe.x
sharpe_return = portfolio_return(sharpe_weights, mean_returns)
sharpe_std = portfolio_std(sharpe_weights, cov_matrix)
sharpe_ratio = portfolio_sharpe(sharpe_weights, mean_returns, cov_matrix, risk_free_rate)

print("Maximum Sharpe Ratio Portfolio:")
print("-" * 50)
for asset, weight in zip(assets, sharpe_weights):
    print(f"{asset}: {weight:.4f} ({weight*100:.2f}%)")
print(f"\nExpected Return: {sharpe_return:.4f} ({sharpe_return*100:.2f}%)")
print(f"Standard Deviation: {sharpe_std:.4f} ({sharpe_std*100:.2f}%)")
print(f"Sharpe Ratio: {sharpe_ratio:.4f}")

Maximum Sharpe Ratio Portfolio:
--------------------------------------------------
Saham A: 0.0493 (4.93%)
Saham B: 0.5661 (56.61%)
Saham C: 0.0394 (3.94%)
Obligasi: 0.3452 (34.52%)

Expected Return: 0.1950 (19.50%)
Standard Deviation: 0.1994 (19.94%)
Sharpe Ratio: 0.8776

Generate Efficient Frontier

# Generate efficient frontier
target_returns = np.linspace(mean_returns.min(), mean_returns.max(), 50)
efficient_portfolios = []

for target in target_returns:
    # Constraint tambahan untuk target return
    constraints_ef = [
        {'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
        {'type': 'eq', 'fun': lambda x: portfolio_return(x, mean_returns) - target}
    ]
    
    result = minimize(
        fun=lambda w: portfolio_variance(w, cov_matrix),
        x0=initial_weights,
        method='SLSQP',
        bounds=bounds,
        constraints=constraints_ef
    )
    
    if result.success:
        efficient_portfolios.append({
            'return': target,
            'std': portfolio_std(result.x, cov_matrix),
            'weights': result.x
        })

# Extract data untuk plotting
ef_returns = [p['return'] for p in efficient_portfolios]
ef_stds = [p['std'] for p in efficient_portfolios]

# Generate random portfolios untuk comparison
n_random = 5000
random_portfolios = []

for _ in range(n_random):
    w = np.random.random(n_assets)
    w /= np.sum(w)
    random_portfolios.append({
        'return': portfolio_return(w, mean_returns),
        'std': portfolio_std(w, cov_matrix)
    })

random_returns = [p['return'] for p in random_portfolios]
random_stds = [p['std'] for p in random_portfolios]

# Plot
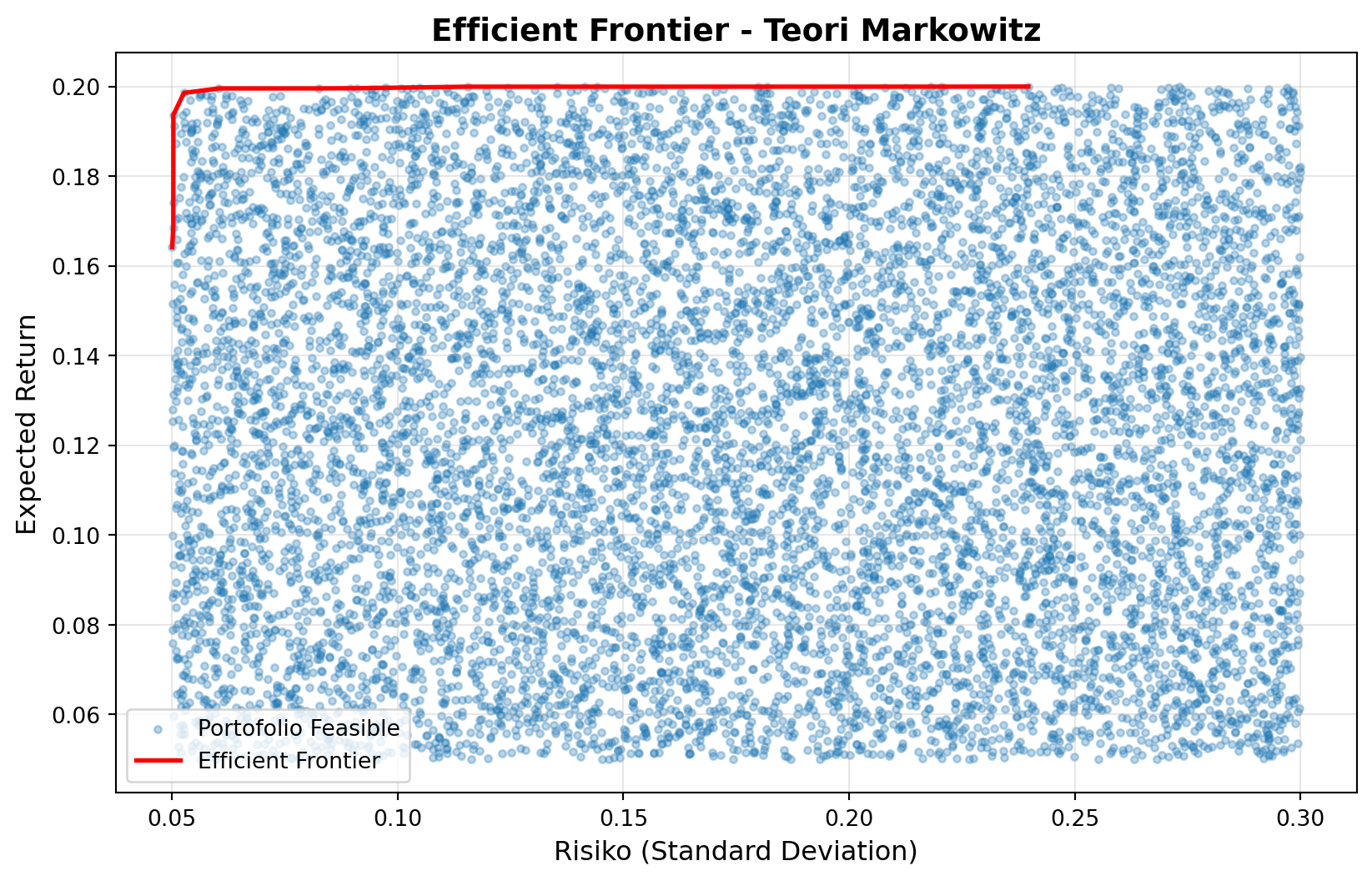
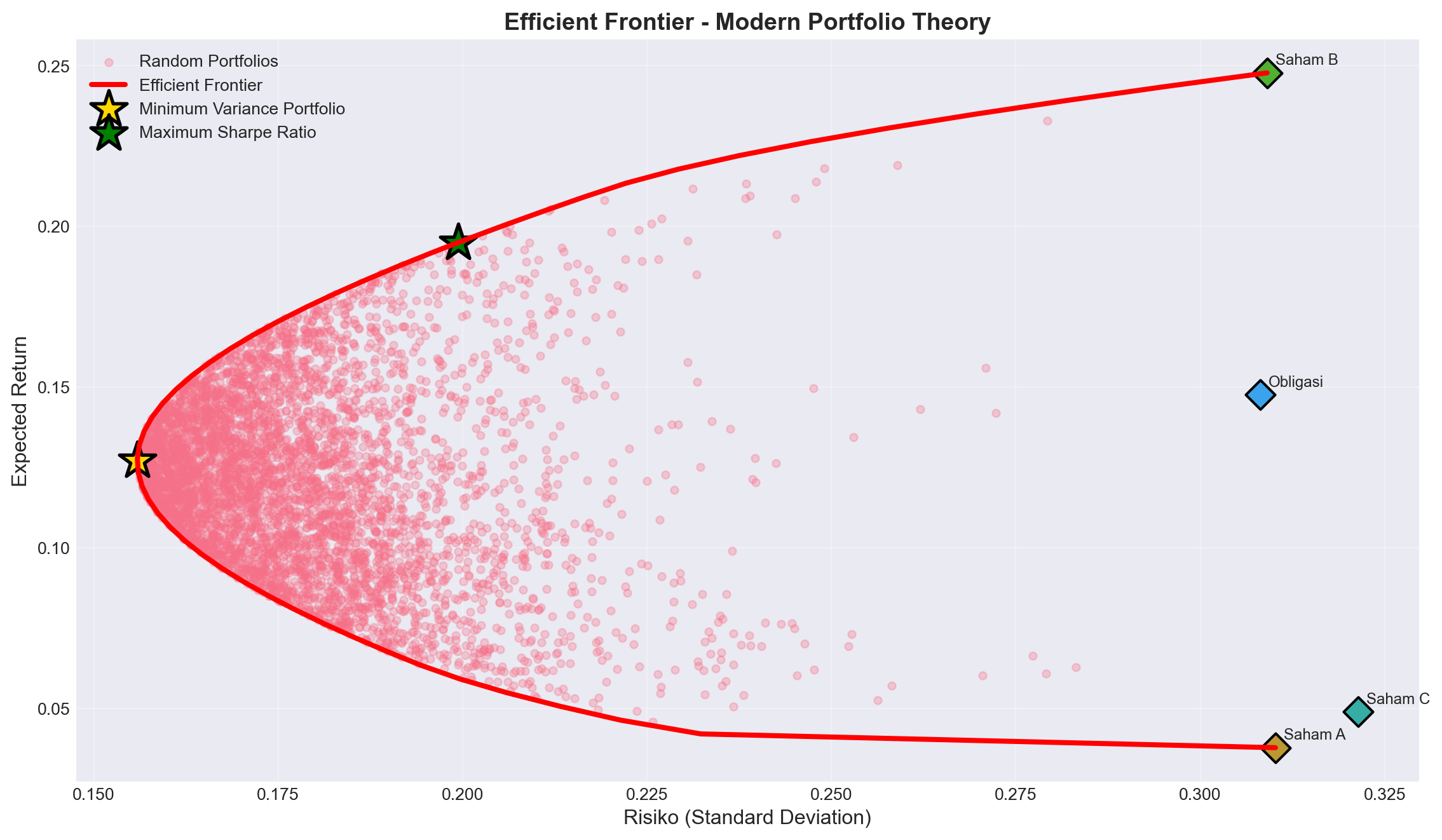
plt.figure(figsize=(12, 7))
plt.scatter(random_stds, random_returns, alpha=0.3, s=20, label='Random Portfolios')
plt.plot(ef_stds, ef_returns, 'r-', linewidth=3, label='Efficient Frontier')
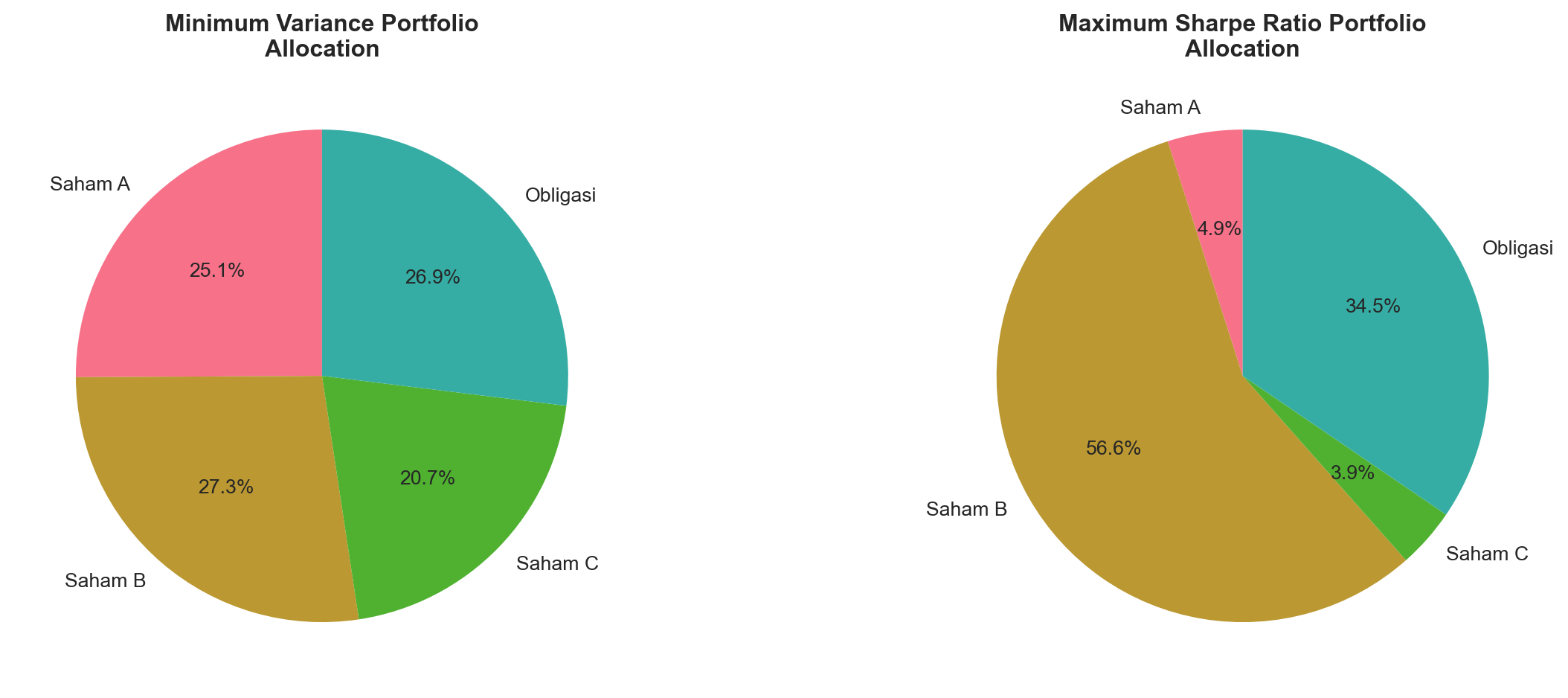
plt.scatter(mvp_std, mvp_return, marker='*', s=500, c='gold', 
           edgecolors='black', linewidths=2, label='Minimum Variance Portfolio')
plt.scatter(sharpe_std, sharpe_return, marker='*', s=500, c='green',
           edgecolors='black', linewidths=2, label='Maximum Sharpe Ratio')

# Plot individual assets
for i, asset in enumerate(assets):
    plt.scatter(np.sqrt(cov_matrix.iloc[i, i]), mean_returns[i], 
               marker='D', s=150, edgecolors='black', linewidths=1.5)
    plt.annotate(asset, (np.sqrt(cov_matrix.iloc[i, i]), mean_returns[i]),
                xytext=(5, 5), textcoords='offset points', fontsize=9)

plt.xlabel('Risiko (Standard Deviation)', fontsize=12)
plt.ylabel('Expected Return', fontsize=12)
plt.title('Efficient Frontier - Modern Portfolio Theory', fontsize=14, fontweight='bold')
plt.legend(loc='best', fontsize=10)
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

Figure 11.1: Efficient Frontier dengan Data Simulasi

Visualisasi Alokasi Aset

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

# MVP allocation
ax1.pie(mvp_weights, labels=assets, autopct='%1.1f%%', startangle=90)
ax1.set_title('Minimum Variance Portfolio\nAllocation', fontweight='bold')

# Max Sharpe allocation
ax2.pie(sharpe_weights, labels=assets, autopct='%1.1f%%', startangle=90)
ax2.set_title('Maximum Sharpe Ratio Portfolio\nAllocation', fontweight='bold')

plt.tight_layout()
plt.show()

Figure 11.2: Perbandingan Alokasi Aset

12 Keterbatasan dan Kritik MPT

Keterbatasan Utama

1. Asumsi Distribusi Normal
   • Return aset sering menunjukkan fat tails dan skewness
   • Mengabaikan kejadian ekstrem (black swan events)
2. Estimasi Parameter
   • Sangat sensitif terhadap estimasi expected return
   • Historical data tidak selalu memprediksi future returns
3. Single Period Framework
   • Tidak mempertimbangkan multi-period rebalancing
   • Mengabaikan path-dependency
4. Mengabaikan Transaction Costs
   • Biaya transaksi dan pajak dapat signifikan
   • Rebalancing memiliki cost
5. Liquidity dan Market Impact
   • Tidak mempertimbangkan likuiditas
   • Portfolio besar dapat mempengaruhi harga

Alternatif dan Pengembangan

• Black-Litterman Model: Menggabungkan market equilibrium dengan investor views
• Risk Parity: Alokasi berdasarkan kontribusi risiko
• Factor Models: Fama-French, momentum, dll
• Robust Optimization: Mengatasi ketidakpastian parameter
• Behavioral Portfolio Theory: Mempertimbangkan aspek behavioral

13 Kesimpulan

Kontribusi Penting MPT

1. Framework Kuantitatif: Memberikan pendekatan sistematis untuk diversifikasi
2. Trade-off Risk-Return: Mengkuantifikasi hubungan risiko dan return
3. Optimal Diversification: Menunjukkan manfaat diversifikasi secara matematis
4. Foundation untuk Teori Modern: Dasar bagi CAPM, APT, dan lainnya

Praktik Terbaik

• Gunakan MPT sebagai starting point, bukan solusi final
• Kombinasikan dengan fundamental analysis
• Regular rebalancing dengan mempertimbangkan transaction costs
• Stress testing dan scenario analysis
• Pertimbangkan faktor-faktor tambahan (ESG, momentum, dll)

Referensi

1. Markowitz, H. (1952). “Portfolio Selection”. Journal of Finance, 7(1), 77-91.
2. Markowitz, H. (1959). Portfolio Selection: Efficient Diversification of Investments. John Wiley & Sons.
3. Sharpe, W. F. (1964). “Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk”. Journal of Finance, 19(3), 425-442.
4. Elton, E. J., Gruber, M. J., Brown, S. J., & Goetzmann, W. N. (2014). Modern Portfolio Theory and Investment Analysis. John Wiley & Sons.
5. Bodie, Z., Kane, A., & Marcus, A. J. (2021). Investments. McGraw-Hill Education.

---

Catatan: Dokumen ini dibuat untuk tujuan edukasi. Implementasi aktual memerlukan data real-time, analisis fundamental, dan pertimbangan kondisi pasar terkini.